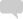Theorem: log(-1) = 0
Proof:
a. log[(-1)^2] = 2 * log(-1)

On the other hand:
b. log[(-1)^2] = log(1) = 0

Combining a) and b) gives:
2* log(-1) = 0
Divide both sides by 2:
log(-1) = 0

Theorem: 4 = 5
Proof:
-20 = -20
16 – 36 = 25 – 45
4^2 – 9*4 = 5^2 – 9*5
4^2 – 9*4 + 81/4 = 5^2 – 9*5 + 81/4
(4 – 9/2)^2 = (5 – 9/2)^2
4 – 9/2 = 5 – 9/2
4 = 5

Theorem: All numbers are equal.
Proof: Choose arbitrary a and b, and let t = a + b. Then

a + b = t
(a + b)(a – b) = t(a – b)
a^2 – b^2 = ta – tb
a^2 – ta = b^2 – tb
a^2 – ta + (t^2)/4 = b^2 – tb + (t^2)/4
(a – t/2)^2 = (b – t/2)^2
a – t/2 = b – t/2
a = b

So all numbers are the same, and math is pointless.

Theorem: n=n+1

Proof:
(n+1)^2 = n^2 + 2*n + 1

Bring 2n+1 to the left:
(n+1)^2 – (2n+1) = n^2

Substract n(2n+1) from both sides and factoring, we have:
(n+1)^2 – (n+1)(2n+1) = n^2 – n(2n+1)

Adding 1/4(2n+1)^2 to both sides yields:
(n+1)^2 – (n+1)(2n+1) + 1/4(2n+1)^2 = n^2 – n(2n+1) + 1/4(2n+1)^2

This may be written:
[ (n+1) - 1/2(2n+1) ]^2 = [ n - 1/2(2n+1) ]^2

Taking the square roots of both sides:
(n+1) – 1/2(2n+1) = n – 1/2(2n+1)

Add 1/2(2n+1) to both sides:
n+1 = n

Theorem: 1 + 1 = 2
Proof:
n(2n – 2) = n(2n – 2)
n(2n – 2) – n(2n – 2) = 0
(n – n)(2n – 2) = 0
2n(n – n) – 2(n – n) = 0
2n – 2 = 0
2n = 2
n + n = 2
or setting n = 1
1 + 1 = 2